1.13 Von Neumann, l’architecte de l’ordinateur moderne

John von Neumann (1903-1957) était un homme impressionnant. Nous avons affaire à un homme capable de mémoriser des livres entiers et de se les remémorer des années plus tard. La mémoire était chez von Neumann une seconde nature. Plus encore, il était un authentique calculateur prodige. Il était capable de calculer mentalement en quelques secondes ce que d’autres pouvaient prendre une journée à faire sur papier. Les mathématiques étaient pour lui une troisième nature. « Si les gens ne croient pas que les mathématiques sont simples, c’est uniquement parce qu’ils ne réalisent pas à quel point la vie est compliquée » aurait-il dit un jour. Il était un homme pour qui les analogies mathématiques donnaient à chaque instant un sens à la vie.

À la fin de l’été 1944, von Neumann fait la connaissance du capitaine Herman H. Goldstine, un militaire qui travaille sur une machine à calculer surnommé l’ENIAC construite dans les laboratoires de la Moore School of Electrical Engineering de l’université de Pennsylvanie. Von Neumann était alors consultant en balistique pour l’armée américaine et il était justement à la recherche d’une puissante machine à calculer. L’ENIAC avait tout pour lui plaire. Bien vite, il la mobilise pour ses besoins et intègre l’équipe d’ingénieurs menée par Eckert et Mauchly. Ceux-ci sont déjà penchés sur les plans d’une autre machine qui devrait résoudre plusieurs problèmes de conception posés par l’ENIAC. Leur collaboration est de l’avis de tous extrêmement fructueuse et culmine dans la rédaction par von Neumann au printemps 1945 d’une première ébauche de rapport sur l’EDVAC (voir note 10).

Pour comprendre l’innovation de von Neumann, il faut examiner ce qui différencie l’ENIAC de l’EDVAC. En 1944, l’ENIAC était la premier calculateur digital entièrement électronique. Il était un pur rejeton du mémoire de maîtrise de Shannon, puisque l’électronique permettait maintenant des calculs booléens extrêmement rapides. La méthode de calcul était binaire, conformément à la logique booléenne de Shannon. Le design de l’ENIAC mettait à profit la possibilité de calculer un nouveau patron de circuits capable de résoudre toute équation mathématique. L’ENIAC pouvait ainsi être reprogrammé, c’est-à-dire qu’il était possible de changer manuellement la circuiterie de la machine (l’organisation des relais et des commutateurs), tout comme la machine analytique de Babbage pouvait lire un patron de calcul différent pour chaque type de calcul. L’ENIAC est programmable, mais la programmation se fait à la main en organisant des circuits composés de dizaines d’interrupteurs et de câbles. Une équipe de six femmes programmeuses était chargée de faire ce travail. (Pour en savoir plus sur ces pionnières de l'informatique : http://www.witi.com/center/witimuseum/halloffame/1997/eniac.php) En ce sens, l’ENIAC n’est pas tout à fait une machine universelle de Turing, au sens où l’algorithme des instructions n’est pas directement traduisible dans le langage de la machine. L’ENIAC ne peut « lire » le code d’instructions d’une autre machine et l’exécuter à sa place. Il faut avoir recours à des programmeuses qui change à la main le câblage et la circuiterie de la machine, et par conséquent l’algorithme des instructions de calcul.

Inspiré par l’universalité de la machine de Turing, von Neumann cherche le moyen de faire une machine électronique « tout-usage » (all purpose). Cela signifie que la machine utilise une circuiterie universelle qui lui permet de lire et d’appliquer les instructions (l’algorithme) de tout autre machine à calculer. L’ENIAC avait déjà une mémoire pour stocker les résultats des calculs intermédiaires. Cette mémoire ne contient donc que des données numériques. L’idée que von Neumann met sur papier propose de stocker également les instructions de l’algorithme de calcul numérique dans la même mémoire que celle des données numériques. Il devient alors possible de programmer numériquement, et non plus manuellement, la machine à calculer en question. Plutôt que de recâbler la machine, les programmeuses doivent maintenant traduire l’algorithme directement dans le langage numérique de la machine. L’algorithme a maintenant le même statut que les données numériques à calculer. L’algorithme devient lui aussi mémorisable, il devient programme stockable dans une mémoire électronique.

Dans son rapport de 1945, von Neumann propose une architecture matérielle de la machine à calculer en cinq parties. La première est l’unité arithmétique, elle permet de calculer les opérations arithmétiques de base ainsi que certaines fonctions arithmétiques plus compliquées (racine, logarithme, etc.). La seconde partie est l’unité de contrôle. Cette unité ordonne les données numériques à calculer par l’unité arithmétique. Autrement dit, c’est l’unité qui est responsable de l’application de l’algorithme de calcul. Dans l’ENIAC, cette partie était uniquement programmable à la main. Dans l’ébauche de rapport de von Neumann, elle devient programmable par instructions digitales stockées en mémoire. La mémoire constitue la troisième unité. Dans l’ENIAC, elle ne stockait que les données numériques calculées par l’unité arithmétique. Dans l’EDVAC, elle stocke à la fois ces premières et les instructions codées numériquement qui programment l’unité de contrôle. Ensuite viennent les deux dernières unités, l’unité d’entrée et l’unité de sortie de données, elles servent à acquérir les données à calculer et transférer celles calculées vers les périphériques d’entrée (clavier, souris, pour prendre des exemples contemporains) et de sortie (écran, imprimante). À peu de choses près, cette architecture est celle commune à la grande majorité des ordinateurs personnels. Aujourd’hui, l’unité arithmétique exécute en plus des opérations logiques. L’autre ajout notable est celui d’antémémoires (ou caches) qui permettent un accès plus rapide aux données mémorisées. Les prochains schémas permettent de comparer les architectures de l’ENIAC, de von Neumann et des ordinateurs contemporains.

Figure 2: Comparaison entre trois différentes architectures d'ordinateur


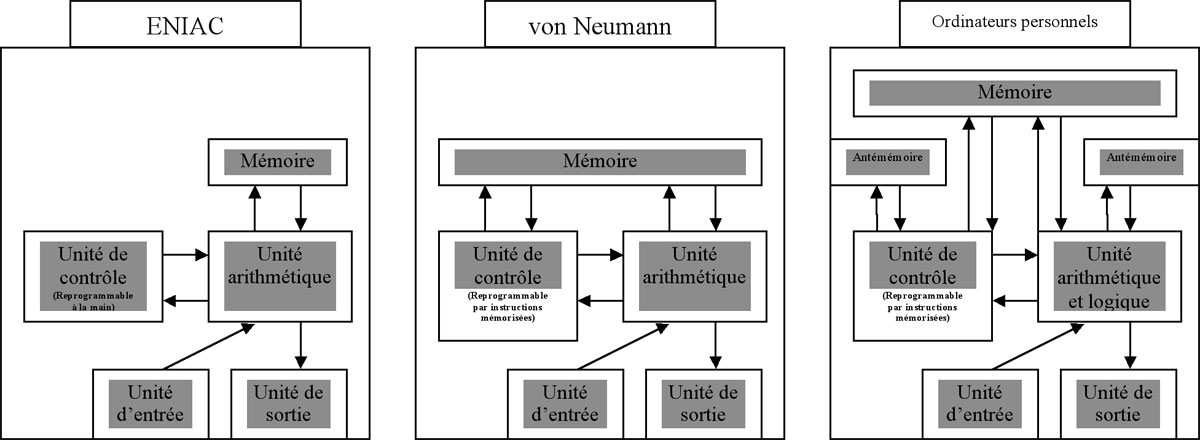
Figure 2: Comparaison entre trois différentes architectures d'ordinateur

Selon Howard Gardner, von Neumann déduit de l’article de McCulloch et Pitts que « tout ce qui peut être décrit de manière exhaustive et sans ambiguïté […] peut être conçu comme un réseau neuronal approprié. » Aussi il adopte dans son ébauche de rapport un vocabulaire qui emploie couramment l’analogie entre les activités et composantes neuronales du cerveau et celles de l’EDVAC.

Von Neumann nomme « E-element » le modèle de neurone simplifié de Pitts et McCulloch et la description qu’il donne du câblage de sa machine fait bien sûr penser aux écrits d’un neurophysiologiste : « [Le E-element] sera représenté par un cercle, O, qui reçoit des stimuli excitateurs ou inhibants et qui émet ses propres stimuli suivant une ligne qui lui est attachée : O– » (Segal 2003, pp.171-172)

Le câblage dont il est question ici est la circuiterie d’une machine universelle de Turing ou tout-usage de von Neumann. Ce recours à un vocabulaire emprunté au physiologiste lui permet de se libérer des contraintes purement techniques de l’ingénieur. Grâce à l’analogie, il peut dissocier les patrons de calcul de leur description matérielle sous forme de circuiterie électrique.

Si von Neumann se laisse inspirer par l’analogie entre la circuiterie de la machine et le réseau neuronal du cerveau, il ne le fera pas toujours avec le même enthousiasme débordant que McCulloch. Von Neumann exprime bien ses difficultés dans une lettre datant de 1946.

What seems worth emphasizing to me is, however, that after the great positive contribution of Turing-cum-Pitts-and-McCulloch is assimilated, the situation is rather worse than before. Indeed, these authors have demonstrated in absolute and hopeless generality, that anything and everything Brouwerian can be done by an appropriate mechanism, and specifically by a neural mechanism—and that even one, definite mechanism can be “universal.” Inverting the argument : Nothing that we may know or learn about the functioning of the organism can give, without “microscopic”, cytological work any clues regarding the further details of the neural mechanism…. I think you will feel with me the type of frustration that I am trying to express.
To understand the brain with neurological methods seems to me about as hopeful as to want to understand the ENIAC with no instrument at one’s disposal that is smaller than about 2 feet across its critical organs… (Aspray 1990, pp.184-185)

Von Neumann exprime ici sa croyance en une version assez radicale de la thèse de Church-Turing. Les phénomènes physiques mesurables et calculables sont mécanisables et vice versa. En particulier, puisque le domaine physique inclut aussi le domaine neurobiologique, nous pouvons mécaniser le système nerveux. Mais cette mécanisation devient alors dépendante des progrès des sciences biologiques. Pour mécaniser précisément le système nerveux (le cerveau, et par extension métaphorique, l’esprit, la pensée), nous devons le mesurer le plus précisément possible. Il s’agit d’une limite propre aux technologies de mesure, mais aussi d’une limite de la théorie discrète de McCulloch et Pitts. En effet, ceux-ci reconnaissante que leur théorie est incapable de tenir compte de ce qui échappe à ce qui descriptible de manière discrète, c’est-à-dire les phénomènes biologiques continus qui influencent la dynamique des connexions entre les neurones. En somme, la théorie de McCulloch et Pitts ne pourra jamais nous donner une explication complète du cerveau comme machine à calculer électronique.

Cette rebuffade théorique pousse von Neumann à inverser la suggestion de McCulloch et Pitts. Alors que ceux-ci souhaitaient enrichir la neurophysiologie en lui donnant des outils logique, von Neumann suggère plutôt d’enrichir notre logique de nos observations physiologiques. C’est dans cet état d’esprit qu’il développe sa théorie générale des automates, dont je ne dirai rien ici, sinon qu’elle s’inspire de l’organisation et de la reproduction des cellules vivantes et formalise la construction de machines complexes fiables à partir de machines plus simples et moins fiables. Mais nous n’en dirons pas plus ici.